Pairing subgrapHs Using NetworK Environment Equivalence

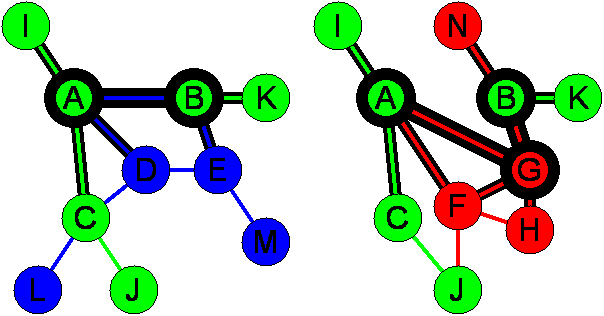
The above diagram illustrates the concept of network context.

Two networks, each from a different species, are shown. Nodes represent a biological entity such as a protein or a metabolic compound. Edges represent an interaction or association between those entities such as a physical interaction between two proteins or an enzyme acting on two compounds. For metabolic networks, edges are labelled with the function of the enzyme acting upon the compound nodes. For protein interaction networks, the edges are unlabelled.

Shared and unshared nodes

In the above diagram, shared nodes in the two networks are coloured green and carry the same label. Blue and red nodes are unshared nodes.

Shared nodes are deemed equivalent nodes in the pair of networks and are determined prior to searching for similar subgraphs. Unshared nodes are those with no equivalent in the other network. The manner in which shared nodes are determined depends on the nature of the biological networks being studied. For metabolic networks, shared nodes are simply identical compounds that exist in both networks. For protein interaction networks, the situation is more complicated because each protein may be similar to many proteins in the other network. PHUNKEE employs two different schemes to allocate shared nodes in protein interaction networks which are described here.

Internal and external nodes

Let us now consider a pair of subgraphs in the two networks by joining nodes A and B via the shortest paths. The nodes that belong to the pair of subgraphs are referred to as internal nodes. The internal nodes are shown above as circles with thick edges (A,B on the left and A,G,B on the right). All other nodes in the network are referred to as external nodes.

Shared and unshared edges

Shared edges are those in each network connecting the same pair of shared nodes (with identical labels, where applicable). In addition, each of the pair of shared nodes must have the same internal/external status in each network. All other edges are unshared edges.

In the above pair of networks, shared edges are coloured green. Unshared edges are coloured red or blue.

Internal and external edges

Internal edges are those that join internal nodes (edges with very thick outline above). For example, the A-B edge in the left subgraph and the A-G and G-B edges in the right subgraph are internal edges. External edges are those that connect internal nodes to external nodes (edges with less thick outline above). For example, the A-I and B-N edges above are external edges.

To determine the similarity of the subgraph pair, we consider each subgraphs network context. The network context of a subgraph is the set of all edges adjoining the internal nodes (shown as edges with a thick outline). A distinction is made between internal edges and external edges. When determining the similarity of network context between the two subgraphs, internal and external edges are given weights w_i and w_e respectively.

Shared-edge ratio

The similarity of subgraph network context is given by the shared-edge ratio. The shared-edge ratio is simply the weighted proportion of highlighted edges that are shared between the two species.

For example, if we take w_i = 1 and w_e = 0.1 for the subgraph pair above:

The number of internal edges: N_i = 3

    shared N_i^shared = 0
    unshared N_i^unshared = 3

The number of external edges: N_e = 12

    shared N_e^shared = 6
    unshared N_e^unshared = 6

The weighted total number of edges is given by:

    N = w_i*N_i + w_e*N_e = 4.2

The weighted total number of shared edges is given by:

    N^shared = w_i*N_i^shared + w_e*N_e^shared = 0.6

The shared-edge ratio is then given by:

    S = N^shared/N = 0.14

Subgraph searching

Of course, this is not the most similar pair of two-node subgraphs to be found in the above networks (For example, the A-C subgraphs are more similar). The PHUNKEE algorithm groups nodes based on subgraph similarity in a greedy fashion until a user-defined maximum number of shared or unshared nodes is reached.